>LINK TO PDF DOWNLOAD<
-
ABSTRACT (Biophysical Journal 116(3):449a
•
February 2019)
Survival Analysis (Proportional Hazard Model) combines elements of Experimental and Observational studies with randomization to treatment group. The recent Estrogen and Progestin Trials ( JAMA 2017, 318(10): 927-938)1 is an 18 year observational follow-up of one such clinical study ( JAMA , July 17, 2002, 288(3):321-333)2. Hormones after menopause had no increased harms according to the update, reversing the original findings. A Linear Regression supported a decreasing Mortality Rate of -3.9/10,000 each additional year on hormone (Menopause 2004;11(6):664(P-43)). Regression informs the data sets, suggests a more restrictive Hypothesis Test at p<=0.01 for Risk Ratios, and the use of Confidence Intervals to achieve more reliable interpretations.
-
BACKGROUND
An ongoing walk back of all Women's Health Initiative Studies (2002-2017) findings has occurred:
-
2002
-
Randomized Intention to treat
Clinical Trial [
CEE
+
MPA
] :
I. "Overall health risks exceeded benefits from use of combined estrogen plus progestin for an average of 5.2 year follow-up among healthy postmenopausal US women." 2
II. Menopausal women were warned to stop their hormones based on the highly-publicized findings of the WHI 2002 and subsequent papers. The use of estrogen-only therapy in U.S. women aged 50 to 59 declined nearly 79 percent between 2001 and 2011 . It is estimated during that time, at least 18,000 excess deaths occurred because of estrogen avoidance and possibly more than 91,000." 5
-
2017
- 18 year
Observational follow-up
[
CEE
or
CEE
+
MPA
]
1
:
I. " hormone therapy with CEE plus MPA for a median of 5.6 years or with CEE alone for a median of 7.2 years was not associated with risk of all-cause, cardiovascular, or cancer mortality during a cumulative follow-up of 18 years. "
II. Peri-menopausal Women (50-59 years) who took [ CEE plus MPA ] showed a Decreased Mortality when compared to Post-menopausal Women (70-79 years) in both periods.
1) Ratio = 0.61[0.43-0.87] (5 year CEE + MPA hormone - intervention phase)
2) Ratio = 0.87[0.76-1.00] (5 year intervention plus 13 year post hormone)
-
2002
-
Randomized Intention to treat
Clinical Trial [
CEE
+
MPA
] :
-
FINDINGS
-
In any regression
or time series analysis, it is important to consider both systematic and stochastic errors. Hazard Ratios are measures of association widely used in prospective studies, "comparing the hazard function among exposed to the hazard function among non-exposed... a hazard ratio of 1 means lack of association, a hazard ratio greater than 1 suggests an increased risk, and a hazard ratio below 1 suggests a smaller risk."
6
-
In the Proportional Hazard Ratio Model
(Cox)
WHI
Prempro
studies, a ratio is reported for the [event rate(numerator y)] to [time-to-event rate(denominator x)] during each time period (year-t) comparing the Hormone(treatment) and Placebo(control) groups:
HR(annualized) = Avg(year-t) = Avg[ EP (year-t) / PL(year-t) ]
-
This obligates:
1) The [HR(year-t)] are constant and randomly distributed over the study.
2) The Deviations in [HR(year-t)] are also randomly (normally) distributed.
-
Some of the biases
in the Survival Analysis data have been identified and informed by the Mortality Difference
3
:
1) Both Group Rates (exposed/unexposed) increase over time in an exponential fashion. This is usually treated statistically by evaluation of the ln [HR] rather than the HR itself, which is linear for an exponential. However, this does not guarantee that the Deviations in HR are randomly distributed.
2) The form of the Hazard Function allows adjustment for patients who leave the study. For instance, un-blinding due to uterine bleeding dropped them out of the Study, and are called "Censored" patients. These would not be counted for a Heart Attack which occurred after the Censoring date.
3)Because the event rates are low, ln [HR] is well approximated by HR. That is, log[exp(t)] is proportional to t, and differences in the ln [HR(t)] are well approximated by differences in [HR( EP-t )-HR(PL-t)].
4) Events identified locally were not confirmed on central adjudication. The 2002 paper published a diagnosis error of (-16%) for MI, (-11%) for PE, (-16%) for DVTs , (-18%) for Cause of Death. When difference in event rates is small, or introduces Group and Time correlation, significance is eroded.
5) Statistical analysis of groups as equal, different, superior, or inferior are not equivalent. This creates confusion in demonstrating Significance.
6) In a multi-Outcome study, Treatment may affect other Outcomes, or introduce a time correlation by advancing or delaying diagnosis. Provera in women is known to alter EKG findings such as noted in Printzmetal's Angina, and so alters diagnosis.
7) The WHI was a carefully constructed multicenter study, patients were randomized at the time of entry into the study. There was up to a six month delay before Hormone/ Placebo) was actually started. For any given year, some patients have less than a full year of treatment compared to control patients who had no treatment for that whole year (no hormone is the same as placebo treatment). Events in a given year are assumed to be randomly distributed throughout the year as having occurred in the midpoint of the year. [Time-to-event] is calculated from entry into the study, not the actual date that hormone treatment begins.
-
In any regression
or time series analysis, it is important to consider both systematic and stochastic errors. Hazard Ratios are measures of association widely used in prospective studies, "comparing the hazard function among exposed to the hazard function among non-exposed... a hazard ratio of 1 means lack of association, a hazard ratio greater than 1 suggests an increased risk, and a hazard ratio below 1 suggests a smaller risk."
6
-
Mortality Results in the
WHI
(2002)
1
-
The 2002
WHI
paper
reported a constant Hazard Ratio of HR=
EP
(Hormone)/PL(Placebo) = 0.98. This produces the following when graphed. It can be seen that the values are not really symmetric about a constant HR = 0.98 as would be expected.
Group has a Year0 bias.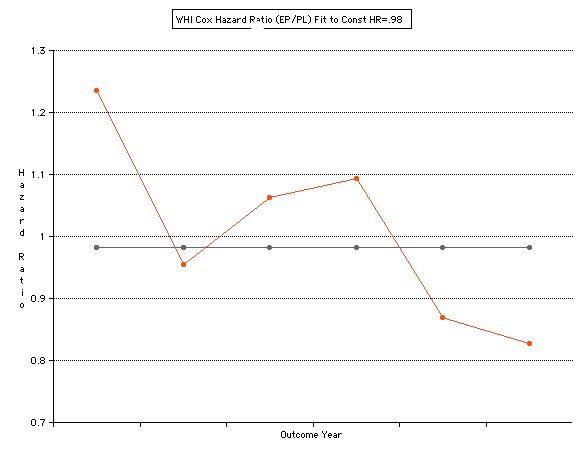
-
The 2002
WHI
paper
reported a constant Hazard Ratio of HR=
EP
(Hormone)/PL(Placebo) = 0.98. This produces the following when graphed. It can be seen that the values are not really symmetric about a constant HR = 0.98 as would be expected.
-
A 2004
WHI
alternative analysis
used a Regression fit to [
EP
(Hormone)-PL(Placebo)] = the Mortality
Difference
. At left the slope is fixed to zero (corresponding the the HR Hazard
Ratio
graph above), on the right intercept and slope parameters are free. Deviation from the Regression line estimated the data errors, a very conservative approach. Note the un-restricted fit has smaller and more symmetric Residuals (32 vs 46, a 44% improvement).
3
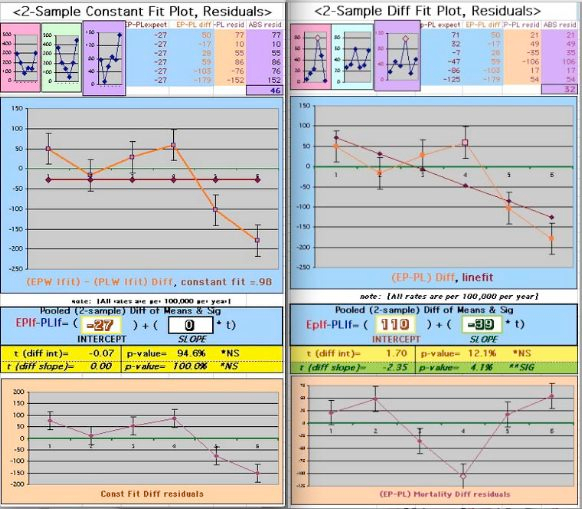
-
The Statistics for the Mortality Difference Regression
shows excellent significance for Slope. Of note, the
Prempro
Intercept shows Significance
diffrent
from zero, contrary to the Placebo fit which indicates that there is poor Intercept estimate different from zero. This supports the idea that the
EP
Group has a Year0 bias.

-
The Annualized Mortality Rate
s from the
WHI
Study (2002)
2
on the left fit with
exponentials
and result in the Hazard Ratio HR Plot at right:
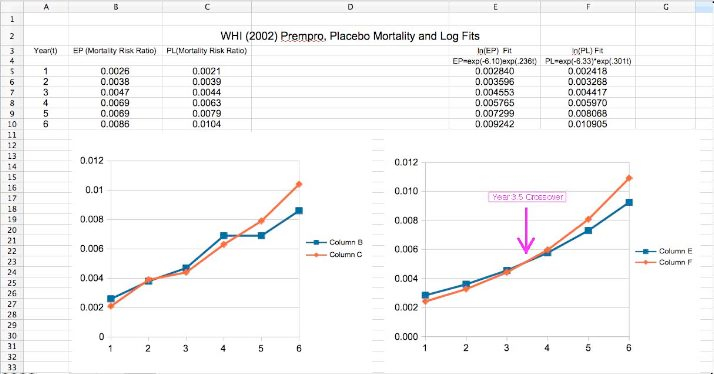
-
Note that there is a crossover at 3.5 years. This is not only a violation of the constant HR assumption, but indicates possible mid-study change (change in sign). Effects of Hormone could be time dependent or there were changes in the Group.
-
Note that there is a crossover at 3.5 years. This is not only a violation of the constant HR assumption, but indicates possible mid-study change (change in sign). Effects of Hormone could be time dependent or there were changes in the Group.
-
Another explanation
can be provided looking at the known higher risk factors in the Hormone Group. Using offsets to the Mortality to equalize the Mortality Rates in each Group to an expected zero at zero time period (Year0 labeled 1), gives the following fits:
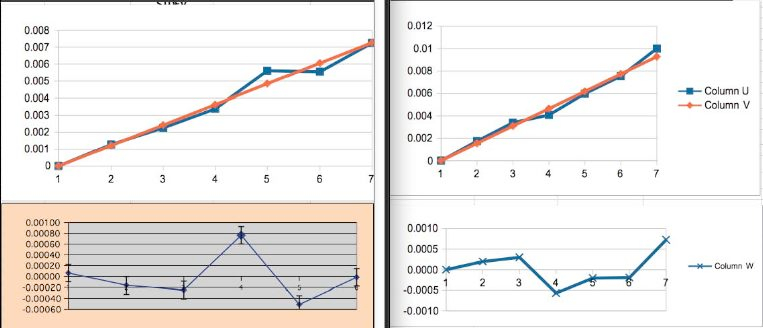
-
This produces a Mortality Rate Difference which is monotonic decreasing from 0:

-
The error in the Slope Difference improves by this and approaches significance:
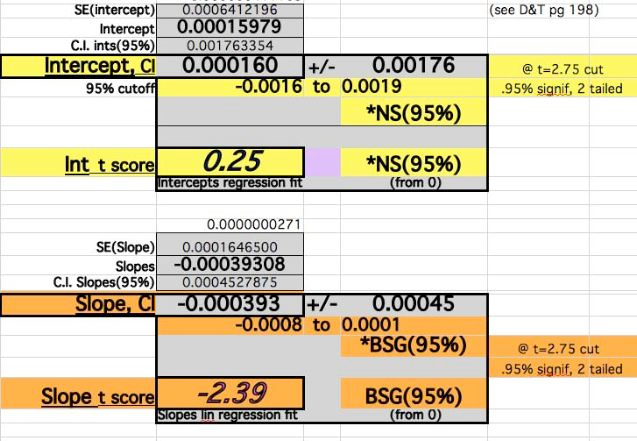
-
This produces a Mortality Rate Difference which is monotonic decreasing from 0:
-
CENSORED DATA DROPOUTS
-
Survival Analysis requires
unblinding
and removal from the study (Censoring). There was a clear jump in censored patients at year 3-4 for reasons. Censoring that removes patients who have not had the identified event yet, would remove the future event and decrease the event rate.
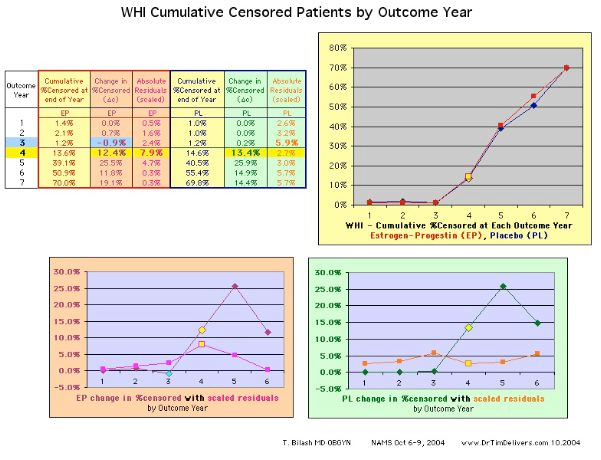
-
The way these are handled is in the Hazard Function,
H = e/(f+c)
where e=Sum(
ei
) event counts for the period i, f=Sum(time to event) for the period i, and c=Sum(time to censored event) for the period i. As noted there was a 15% censor rate in Year4. The expected error in the Hazard function in Year4 is larger than expected. A simple estimate indicates that for a [15%] censor rate one might expect up to a [20%] combined error for the Hazard Rate when data is collected at the a 5% level, 4x the error for each component the usually used in Lab and data evaluations.

-
Quantities being determined are Rates and Ratios of Numbers, not Numbers. An estimate of errors in the Annualized Hazard Ratio as the ratio of Hazard Rates would thus have multiplicative 4x error estimation.

-
Similar results are obtained when considering Confidence Intervals for the Error in a Ratio
6
:
-
For R the Ratio of two numbers with errors:
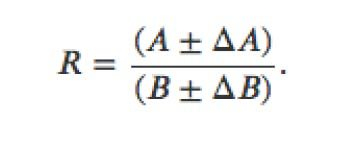
-
The Confidence Interval becomes:
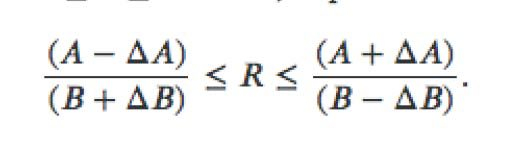
-
Choose
DeltaA
=
DeltaB
= 0.05 (5%) to calculate simple Confidence Interval:
(A-.05A)/(B+.05B) <R< (A+.05A)/(B-.05B)
(.95/1.05)A/B < R < (1.05/.95)A/B
[0.90]A/B <R=A/B<[1.11]A/B
- So, the error in a ratio A/B is ~2x the error in A,B (0.1 for 0.05,0.05)
-
The Hazard Ratio is a Ratio of Rates, so estimating the overall error becomes ~
4x
the error l
evel
chosen.
-
For R the Ratio of two numbers with errors:
-
Survival Analysis requires
unblinding
and removal from the study (Censoring). There was a clear jump in censored patients at year 3-4 for reasons. Censoring that removes patients who have not had the identified event yet, would remove the future event and decrease the event rate.
-
Year 4 is a particularly troublesome value
in the
EP
Hormone group independent of the Rate difference between Groups. The Residual is larger than the other years.
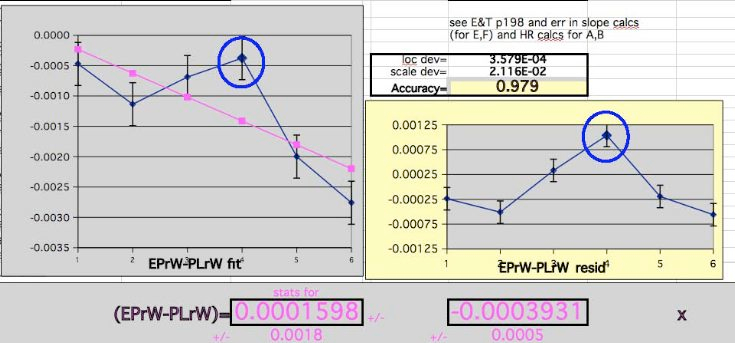
-
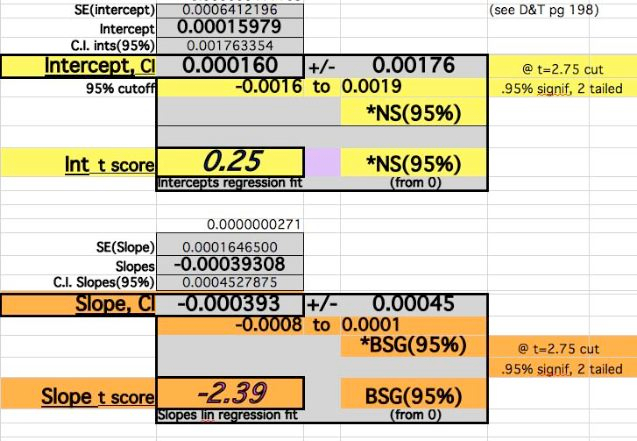
The Regression Fit T-Score for the Slope becomes nearly Significant at the 95% level.
-
As an exercise the regression shifted 30% of the Year4 Rate into Year5 in the
EP
Hormone Group:
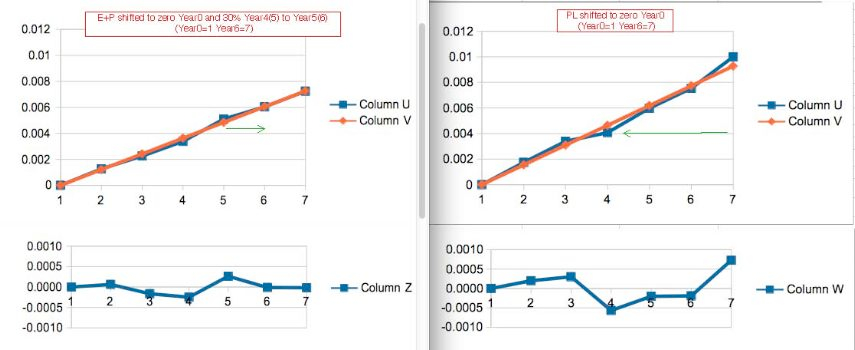
-
Note the improvement in Year4(5) Residual. Note also the indications that some Mortality in the Placebo Group were delayed, or Censored later compared to the Average Mortality Events (bigger denominator in each year).
-
The Regression Fit T-Score for the Slope becomes Significant at the 95% level with these adjustments:
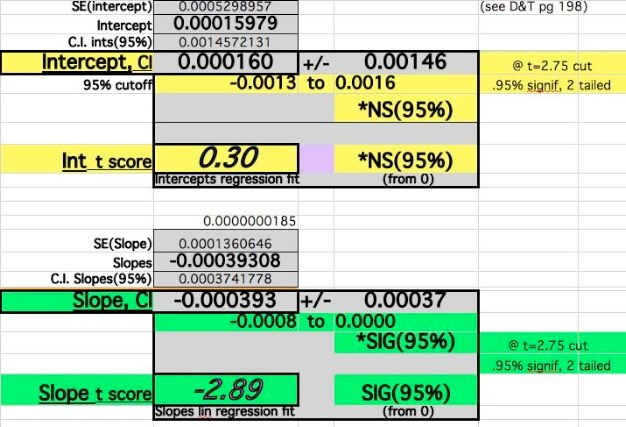
-
Despite the adjustments of 0 events at time 0 and Year4 adjustments, the Slope fit does not vary widely (39-45/100,000). The Year0 errors dominate the Intercept Difference, Year6 dominates the Slope value, and the middle Year values are less
senstive
to both but contributes to the statistical significance.
-
The Regression Fit T-Score for the Slope becomes nearly Significant at the 95% level.
-
CONCLUSIONS
-
A comprehensive explanation of where the
WHI
has taken us appeared in an online news site
1

-
It is telling that the
WHI
Authors rejected evaluations indicating the need for age stratification. The data was not released until 2 years after the publication of the 2002 paper. It is now clear that younger
Perimenopausal
women respond differently to the presence or absence of Hormone, and non-stratification by age injected heterogeneity.
-
Pleas of Clinicians like Holly
Thacker
, MD, went
unheaded
over a 15 year period:
11

-
Patricia T. Kelly, PhD in 2003 suggested the following criteria for
Epidemiologic
Studies (which she argued includes these Intention-to-treat studies Survival Studies):
- want hazard ratio of three or greater. In the WHO, the hazard rates was far less than three, suggesting that factors other than Prempro (Estrogen plus Progestin ) may be responsible.
- want statistically significant difference between study and control group. Statistical significance was not obtained in the WHI .
-
want similar findings in other studies. Another large randomized prospective study,and many retrospective studies did not agree with the
WHI
.
-
Exploratory studies are very important in Medicine, but a large number of large study reversals indicates problems with the statistics. The
heterogeniety
over time and the averaging over different Years assumes there is no change to the cohorts as time goes on. Announcements that treatment is dangerous may be a factor. Discontinuities over time, and excess risk in the treatment group for the
WHI
should have given pause to global recommendations. Overall p-values (p<0.01, 1/4 times the value customarily used for number statistics), or Confidence Intervals (RR >1.5, providing a 4x cushion) might be a reasonable start.
-
A recent paper explored the issue of P-values and
CI
for Relative Risk.
14
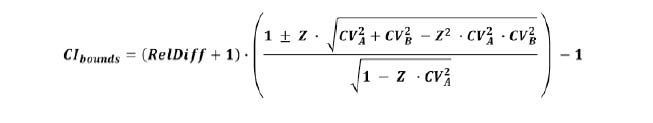
- "despite the apparently ubiquitous inferences about percent change and relative differences there are very few sources that mention how one can calculate the standardized error or confidence interval bounds for such a statistic."
- "there are two factors that affect how badly the naive extrapolation from absolute to relative difference will perform: the size of the true relative difference , and the confidence level ."
- "there is no simple correspondence between a p-value or confidence interval calculated for absolute difference and relative difference (between proportions or means)."
- "I am not aware of a straightforward way for calculating a p-value based on the same approach used to calculate this confidence interval. A p-value calculated with the standard error approximation from the Delta method will be far too conservative"
-
"the issue is not researched enough. The p-value calculation is iterative approximation, there is no analytical solution (formula) we know of"
-
A comprehensive explanation of where the
WHI
has taken us appeared in an online news site
1
-
Moral of the Story?
We should return to "Physiologic Replacement of Hormones" ( PRH ) for Menopause. 13
Show your work, look at the data graphs, cross-check your results.
It should make sense.
-
DEDICATION
This work is dedicated to my undergraduate mentor, Akira Inomata PhD, a brilliant Theoretical Physicist and life-long friend. In addition to his craft, he demonstrates a purpose of will that supports, nurtures and defends both experts and students alike. As he explores Physics, he contributes to Academic, Cultural and Humanitarian causes through his personal engagement.
March 05, 2019
- "Menopausal Hormone Therapy and Long-term All-Cause and Cause-Specific Mortality,
The Women’s Health Initiative Randomized Trials", JoAnn E. Manson et al, JAMA 2017, 318(10): 927-938) - "Risks and Benefits of Estrogen Plus Progestin in Healthy Postmenopausal Women", Writing Group for the Women's Health Initiative Investigators, JAMA , July 17, 2002, 288(3):p321-337
- "Time Dependence of Mortality Rates from Womens
Health Initiative",
North American Menopause Society 15th Annual Meeting, Washington, DC (OCT 2004)
T. Bilash , Menopause 2004;11(6):664(P-43) -
"Hazard Ratio", From: Principles and Practice of Clinical Trial Medicine, 2008,
https://www.sciencedirect.com/topics/medicine-and-dentistry/hazard-ratio -
"The Mortality Toll of Estrogen Avoidance: An Analysis of Excess Deaths Among
Hysterectomized
Women Aged
50 to 59 Years", Philip Sarrel , M.D. et al, July 18, 2013, American Journal of Public Health
http://ajph.aphapublications.org/ doi / pdf /10.2105/ AJPH .2013.301295 -
"Error in ratio of 2 numbers",
https://math.stackexchange.com/questions/1173971/error-in-ratio-of-two-numbers -
"Confidence Intervals for the Risk Ratio (Relative Risk)",
http://sphweb.bumc.bu.edu/ otlt /MPH-Modules/BS/BS704_Confidence_Intervals/BS704_Confidence_Intervals8.html -
"Propagation of error in log ratios",
https://stats.stackexchange.com/questions/324957/propagation-of-error-in-log-ratios -
"San Francisco Medical Society |
WHI
Study: One Year Later",
Patricia T. Kelly, PhD (2003)
( http://www.sfms.org ) -
"
Epidemiology
Faces Its Limits",
Gary Taubes , Science, New Series, Vol. 269, No. 5221 ( Jul . 14, 1995), pp. 164-165+167-169
https://www.huffpost.com/entry/menopause-hormone-replacement-and-mortality-a-research_n_59c51bf1e4b0b7022a6469d3 -
"Menopause, Hormone Replacement And Mortality: A Research Reality Check",
David L. Katz, M.D., M.P.H . in The Huffington Post, Sept 22, 2017
https://www.huffpost.com/entry/menopause-hormone-replacement-and-mortality-a-research_n_59c51bf1e4b0b7022a6469d3 - "In the latest report from the WHI
, the data contradict the conclusions"
Holly Thacker , MD, OBG Management 02/28/14 -
"Menopause, Hormone Replacement And Mortality: A Research Reality Check"
9/22/2017/updated Sep 22, 2017
https://www.huffpost.com/entry/menopause-hormone-replacement-and-mortality-a-research_n_59c51bf1e4b0b7022a6469d3 - Experience suggests the term "Physiologic Replacement of Hormones - PRH for Menopausal Hormone Treatments, in Primary Ovarian Insufficiency, American College of Obstetricians and Gynecologists - Committee Opinion on Hormone Therapy Number 698 • May 2017
-
"Confidence Intervals & P-values for Percent Change / Relative Difference",
Georgi Georgiev , Jan 17, 2019 (online)
http://blog.analytics-toolkit.com/2018/ confidence-intervals-p-values-percent-change-relative-difference / -
Poster available online at:
https://drtimdelivers.com/
whimortality2017_files/WHIposter10.06.04.shtml
(Link Updated 3/14/2024)