?

THE PROPORTIONAL HAZARD MODEL IN RANDOMIZED STUDIES - STATISTICAL INSIGHTS INTO THE WOMEN'S HEALTH INITIATIVE STUDIES (2002-2017) USING REGRESSION ANALYSIS OF MORTALITY.

Timothy D. Bilash , M.D., M.S., F.A.C.O.G
Biophysical Society Annual Meeting (2215-POS B579)
March 2-6, 2019

>LINK TO PDF DOWNLOAD<

ABSTRACT (Biophysical Journal 116(3):449a ^• February 2019)

Survival Analysis (Proportional Hazard Model) combines elements of Experimental and Observational studies with randomization to treatment group. The recent Estrogen and Progestin Trials ( JAMA 2017, 318(10): 927-938)¹ is an 18 year observational follow-up of one such clinical study ( JAMA , July 17, 2002, 288(3):321-333)². Hormones after menopause had no increased harms according to the update, reversing the original findings. A Linear Regression supported a decreasing Mortality Rate of -3.9/10,000 each additional year on hormone (Menopause 2004;11(6):664(P-43)). Regression informs the data sets, suggests a more restrictive Hypothesis Test at p<=0.01 for Risk Ratios, and the use of Confidence Intervals to achieve more reliable interpretations.
BACKGROUND

An ongoing walk back of all Women's Health Initiative Studies (2002-2017) findings has occurred:
1. 2002 - Randomized Intention to treat Clinical Trial [ CEE + MPA ] :
  
  I. "Overall health risks exceeded benefits from use of combined estrogen plus progestin for an average of 5.2 year follow-up among healthy postmenopausal US women." ²
  
  II. Menopausal women were warned to stop their hormones based on the highly-publicized findings of the WHI 2002 and subsequent papers. The use of estrogen-only therapy in U.S. women aged 50 to 59 declined nearly 79 percent between 2001 and 2011 . It is estimated during that time, at least 18,000 excess deaths occurred because of estrogen avoidance and possibly more than 91,000." ⁵
2. 2017 - 18 year Observational follow-up [ CEE or CEE + MPA ] ¹ :
  
  I. " hormone therapy with CEE plus MPA for a median of 5.6 years or with CEE alone for a median of 7.2 years was not associated with risk of all-cause, cardiovascular, or cancer mortality during a cumulative follow-up of 18 years. "
  
  II. Peri-menopausal Women (50-59 years) who took [ CEE plus MPA ] showed a Decreased Mortality when compared to Post-menopausal Women (70-79 years) in both periods.
  
  1) Ratio = 0.61[0.43-0.87] (5 year CEE + MPA hormone - intervention phase)
  2) Ratio = 0.87[0.76-1.00] (5 year intervention plus 13 year post hormone)
FINDINGS
1. In any regression or time series analysis, it is important to consider both systematic and stochastic errors. Hazard Ratios are measures of association widely used in prospective studies, "comparing the hazard function among exposed to the hazard function among non-exposed... a hazard ratio of 1 means lack of association, a hazard ratio greater than 1 suggests an increased risk, and a hazard ratio below 1 suggests a smaller risk." ⁶
2. In the Proportional Hazard Ratio Model (Cox) WHI Prempro studies, a ratio is reported for the [event rate(numerator y)] to [time-to-event rate(denominator x)] during each time period (year-t) comparing the Hormone(treatment) and Placebo(control) groups:
  
  HR(annualized) = Avg(year-t) = Avg[ EP (year-t) / PL(year-t) ]
3. This obligates:
  
  1) The [HR(year-t)] are constant and randomly distributed over the study.
  2) The Deviations in [HR(year-t)] are also randomly (normally) distributed.
4. Some of the biases in the Survival Analysis data have been identified and informed by the Mortality Difference ³ :
  
  1) Both Group Rates (exposed/unexposed) increase over time in an exponential fashion. This is usually treated statistically by evaluation of the ln [HR] rather than the HR itself, which is linear for an exponential. However, this does not guarantee that the Deviations in HR are randomly distributed.
  
  2) The form of the Hazard Function allows adjustment for patients who leave the study. For instance, un-blinding due to uterine bleeding dropped them out of the Study, and are called "Censored" patients. These would not be counted for a Heart Attack which occurred after the Censoring date.
  
  3)Because the event rates are low, ln [HR] is well approximated by HR. That is, log[exp(t)] is proportional to t, and differences in the ln [HR(t)] are well approximated by differences in [HR( EP-t )-HR(PL-t)].
  
  4) Events identified locally were not confirmed on central adjudication. The 2002 paper published a diagnosis error of (-16%) for MI, (-11%) for PE, (-16%) for DVTs , (-18%) for Cause of Death. When difference in event rates is small, or introduces Group and Time correlation, significance is eroded.
  
  5) Statistical analysis of groups as equal, different, superior, or inferior are not equivalent. This creates confusion in demonstrating Significance.
  
  6) In a multi-Outcome study, Treatment may affect other Outcomes, or introduce a time correlation by advancing or delaying diagnosis. Provera in women is known to alter EKG findings such as noted in Printzmetal's Angina, and so alters diagnosis.
  
  7) The WHI was a carefully constructed multicenter study, patients were randomized at the time of entry into the study. There was up to a six month delay before Hormone/ Placebo) was actually started. For any given year, some patients have less than a full year of treatment compared to control patients who had no treatment for that whole year (no hormone is the same as placebo treatment). Events in a given year are assumed to be randomly distributed throughout the year as having occurred in the midpoint of the year. [Time-to-event] is calculated from entry into the study, not the actual date that hormone treatment begins.
Mortality Results in the WHI (2002) ¹
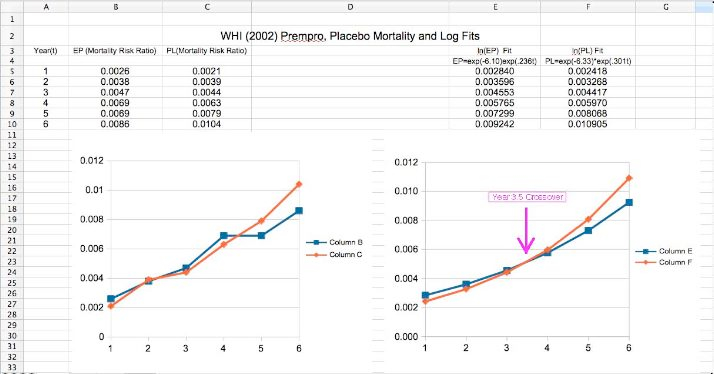
1. The 2002 WHI paper reported a constant Hazard Ratio of HR= EP (Hormone)/PL(Placebo) = 0.98. This produces the following when graphed. It can be seen that the values are not really symmetric about a constant HR = 0.98 as would be expected.
  
  Group has a Year0 bias.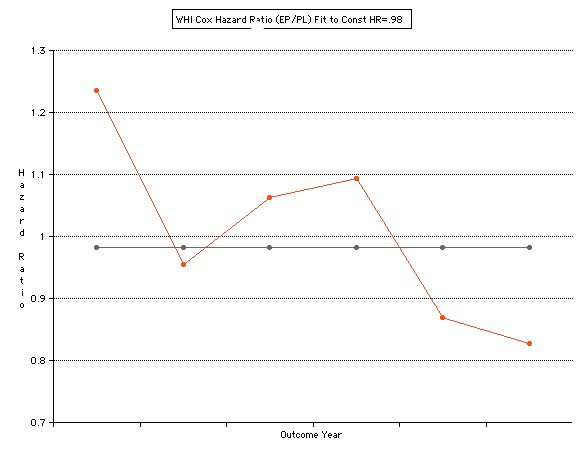
A 2004 WHI alternative analysis used a Regression fit to [ EP (Hormone)-PL(Placebo)] = the Mortality Difference . At left the slope is fixed to zero (corresponding the the HR Hazard Ratio graph above), on the right intercept and slope parameters are free. Deviation from the Regression line estimated the data errors, a very conservative approach. Note the un-restricted fit has smaller and more symmetric Residuals (32 vs 46, a 44% improvement). ³
The Statistics for the Mortality Difference Regression shows excellent significance for Slope. Of note, the Prempro Intercept shows Significance diffrent from zero, contrary to the Placebo fit which indicates that there is poor Intercept estimate different from zero. This supports the idea that the EP Group has a Year0 bias.
The Annualized Mortality Rate s from the WHI Study (2002) ² on the left fit with exponentials and result in the Hazard Ratio HR Plot at right:
1. Note that there is a crossover at 3.5 years. This is not only a violation of the constant HR assumption, but indicates possible mid-study change (change in sign). Effects of Hormone could be time dependent or there were changes in the Group.
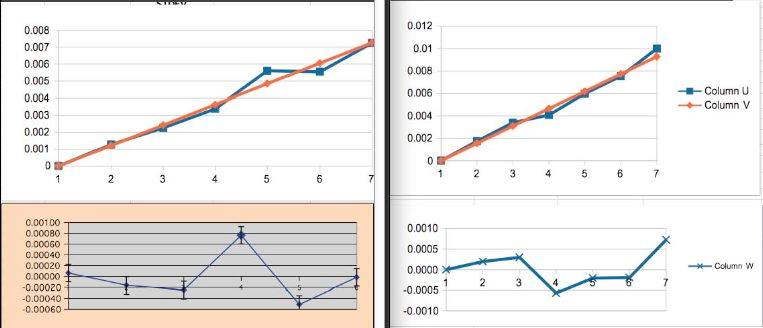
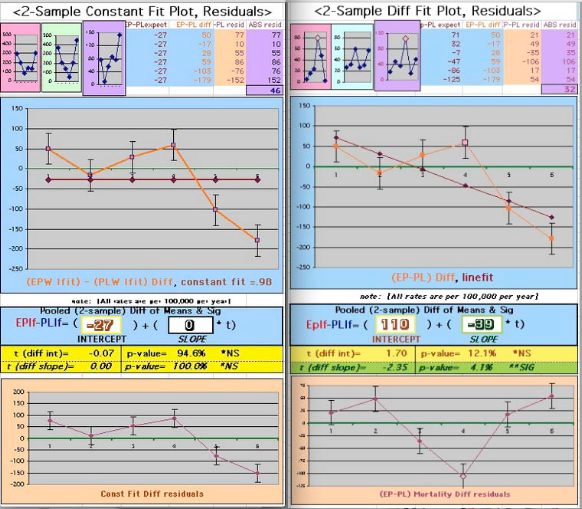
Another explanation can be provided looking at the known higher risk factors in the Hormone Group. Using offsets to the Mortality to equalize the Mortality Rates in each Group to an expected zero at zero time period (Year0 labeled 1), gives the following fits:
1. This produces a Mortality Rate Difference which is monotonic decreasing from 0:
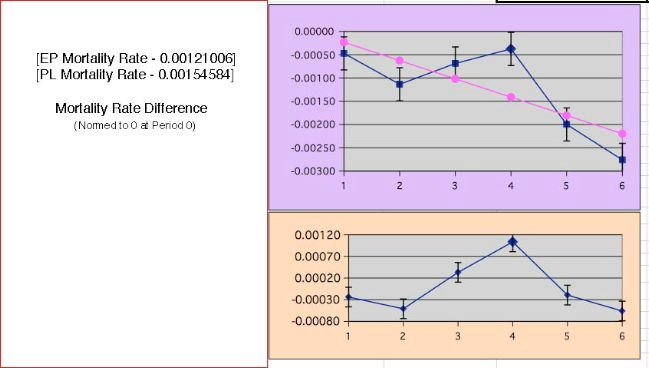
2. The error in the Slope Difference improves by this and approaches significance:
CENSORED DATA DROPOUTS
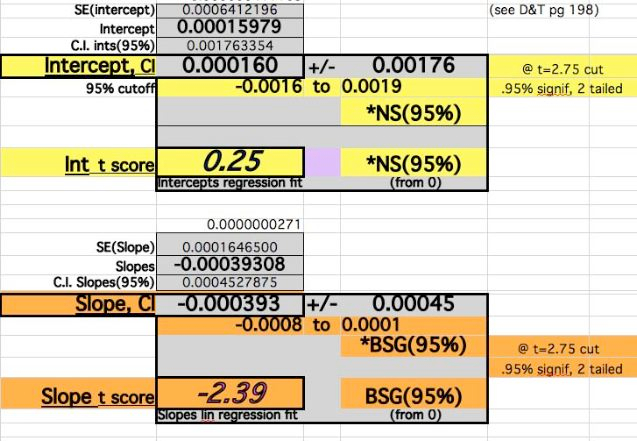
1. Survival Analysis requires unblinding and removal from the study (Censoring). There was a clear jump in censored patients at year 3-4 for reasons. Censoring that removes patients who have not had the identified event yet, would remove the future event and decrease the event rate.
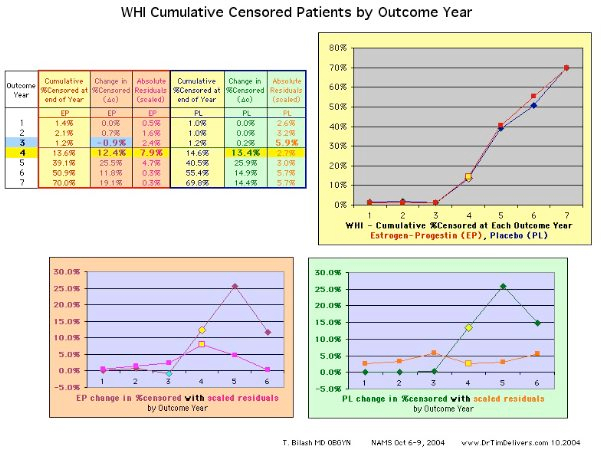
2. The way these are handled is in the Hazard Function, H = e/(f+c) where e=Sum( ei ) event counts for the period i, f=Sum(time to event) for the period i, and c=Sum(time to censored event) for the period i. As noted there was a 15% censor rate in Year4. The expected error in the Hazard function in Year4 is larger than expected. A simple estimate indicates that for a [15%] censor rate one might expect up to a [20%] combined error for the Hazard Rate when data is collected at the a 5% level, 4x the error for each component the usually used in Lab and data evaluations.
3. Quantities being determined are Rates and Ratios of Numbers, not Numbers. An estimate of errors in the Annualized Hazard Ratio as the ratio of Hazard Rates would thus have multiplicative 4x error estimation.
4. Similar results are obtained when considering Confidence Intervals for the Error in a Ratio ⁶ :
  1. For R the Ratio of two numbers with errors:
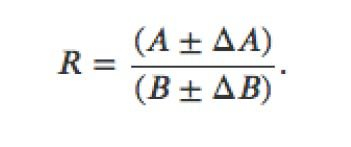
  2. The Confidence Interval becomes:
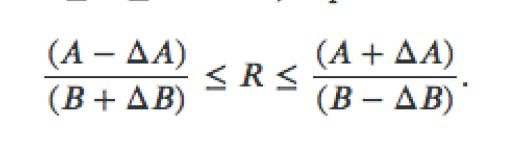
  3. Choose DeltaA = DeltaB = 0.05 (5%) to calculate simple Confidence Interval:
    
    (A-.05A)/(B+.05B) <R< (A+.05A)/(B-.05B)
    (.95/1.05)A/B < R < (1.05/.95)A/B
    [0.90]A/B <R=A/B<[1.11]A/B
  4. So, the error in a ratio A/B is ~2x the error in A,B (0.1 for 0.05,0.05)
  5. The Hazard Ratio is a Ratio of Rates, so estimating the overall error becomes ~ 4x the error l evel chosen.
Year 4 is a particularly troublesome value in the EP Hormone group independent of the Rate difference between Groups. The Residual is larger than the other years.
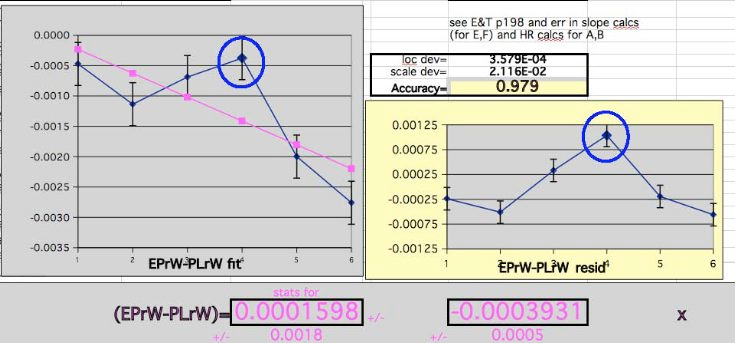
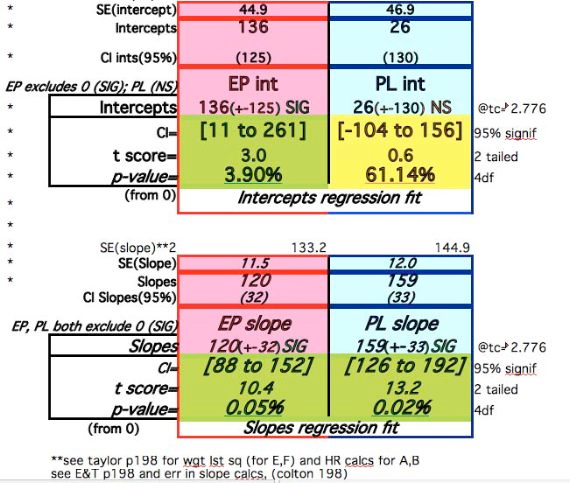
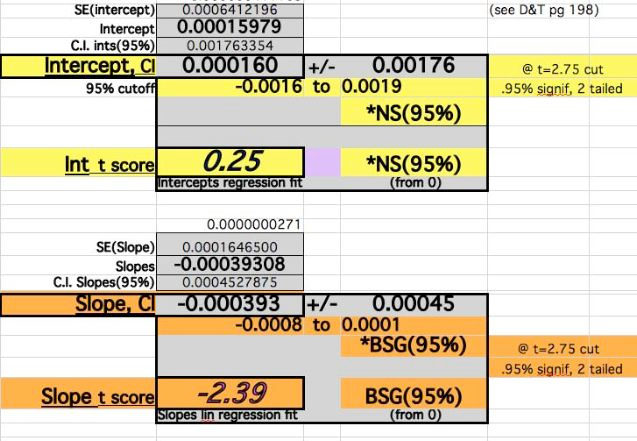
1. The Regression Fit T-Score for the Slope becomes nearly Significant at the 95% level.
2. As an exercise the regression shifted 30% of the Year4 Rate into Year5 in the EP Hormone Group:
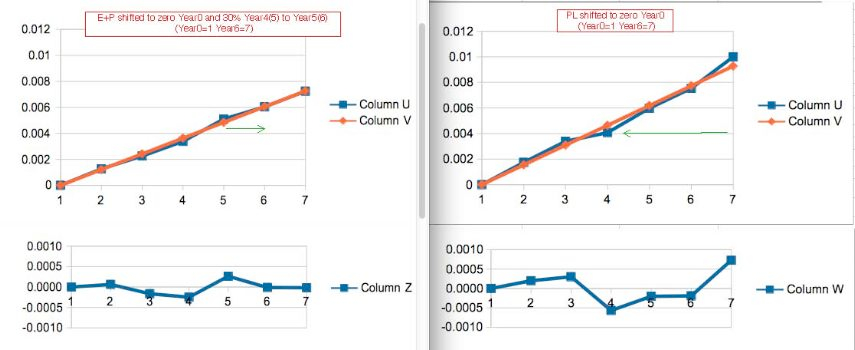
3. Note the improvement in Year4(5) Residual. Note also the indications that some Mortality in the Placebo Group were delayed, or Censored later compared to the Average Mortality Events (bigger denominator in each year).
4. The Regression Fit T-Score for the Slope becomes Significant at the 95% level with these adjustments:
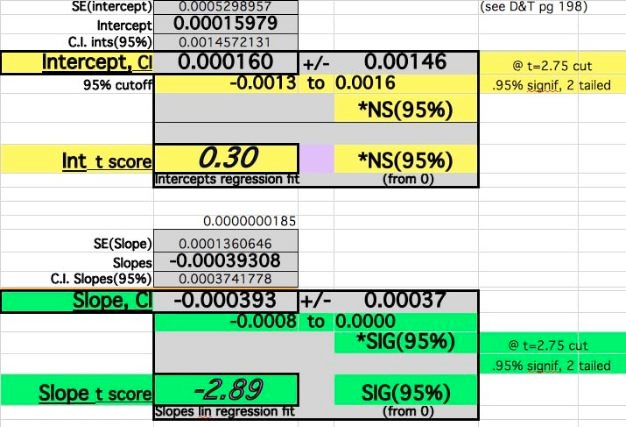
5. Despite the adjustments of 0 events at time 0 and Year4 adjustments, the Slope fit does not vary widely (39-45/100,000). The Year0 errors dominate the Intercept Difference, Year6 dominates the Slope value, and the middle Year values are less senstive to both but contributes to the statistical significance.
CONCLUSIONS
1. A comprehensive explanation of where the WHI has taken us appeared in an online news site ¹
2. It is telling that the WHI Authors rejected evaluations indicating the need for age stratification. The data was not released until 2 years after the publication of the 2002 paper. It is now clear that younger Perimenopausal women respond differently to the presence or absence of Hormone, and non-stratification by age injected heterogeneity.
3. Pleas of Clinicians like Holly Thacker , MD, went unheaded over a 15 year period: ¹¹
4. Patricia T. Kelly, PhD in 2003 suggested the following criteria for Epidemiologic Studies (which she argued includes these Intention-to-treat studies Survival Studies):
  1. want hazard ratio of three or greater. In the WHO, the hazard rates was far less than three, suggesting that factors other than Prempro (Estrogen plus Progestin ) may be responsible.
  2. want statistically significant difference between study and control group. Statistical significance was not obtained in the WHI .
  3. want similar findings in other studies. Another large randomized prospective study,and many retrospective studies did not agree with the WHI .
5. Exploratory studies are very important in Medicine, but a large number of large study reversals indicates problems with the statistics. The heterogeniety over time and the averaging over different Years assumes there is no change to the cohorts as time goes on. Announcements that treatment is dangerous may be a factor. Discontinuities over time, and excess risk in the treatment group for the WHI should have given pause to global recommendations. Overall p-values (p<0.01, 1/4 times the value customarily used for number statistics), or Confidence Intervals (RR >1.5, providing a 4x cushion) might be a reasonable start.
6. A recent paper explored the issue of P-values and CI for Relative Risk. ¹⁴
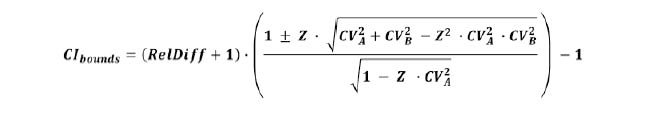
  1. "despite the apparently ubiquitous inferences about percent change and relative differences there are very few sources that mention how one can calculate the standardized error or confidence interval bounds for such a statistic."
  2. "there are two factors that affect how badly the naive extrapolation from absolute to relative difference will perform: the size of the true relative difference , and the confidence level ."
  3. "there is no simple correspondence between a p-value or confidence interval calculated for absolute difference and relative difference (between proportions or means)."
  4. "I am not aware of a straightforward way for calculating a p-value based on the same approach used to calculate this confidence interval. A p-value calculated with the standard error approximation from the Delta method will be far too conservative"
  5. "the issue is not researched enough. The p-value calculation is iterative approximation, there is no analytical solution (formula) we know of"
Moral of the Story?

We should return to "Physiologic Replacement of Hormones" ( PRH ) for Menopause. ¹³
Show your work, look at the data graphs, cross-check your results.
It should make sense.
DEDICATION

This work is dedicated to my undergraduate mentor, Akira Inomata PhD, a brilliant Theoretical Physicist and life-long friend. In addition to his craft, he demonstrates a purpose of will that supports, nurtures and defends both experts and students alike. As he explores Physics, he contributes to Academic, Cultural and Humanitarian causes through his personal engagement.

March 05, 2019